A group of people who have no shared language could sit around and collectively solve a math problem, but people with no shared language could not read the same book. When we think of math, it needs to be seen as a symbolic language, where characters and symbols represent concepts. For instance, there is no such thing as the number four. Four symbolically represents one + one + one + one. It’s the reason children, when learning addition, will move objects like Cheerios into sections so that they can understand the symbolic representation of four.
When my sons were in middle school and younger, Common Core math was being implemented all across the country, partly in response to closing math gaps between boys and girls. The purpose was to help advance girls in math and open up STEM (science, technology, engineering, and math) opportunities for them. And the intentions were well meaning but—like so many educational movements—tend to focus more on girls than boys under the pretext of Title IX, which was never meant to discriminate between boys and girls but to ensure equal opportunities.
Implementing different approaches that help girls thrive is important, but not more important than helping boys thrive. The “new math” moved from math as a symbolic language to a language built on tasks and verbal skills in many instances that required greater communication between both hemispheres of the brain and other skills, where girls—in the aggregate—perform better than boys.
When one of my sons was in elementary school, I started to notice some challenges in his math tests and started looking at his assignments more closely. I sat down with him, and we reviewed the problems he was tasked to solve and the methodology. I realized that my son was not having a problem with math; he was having a problem with an approach that would not serve his boy brain well. Once I introduced a new approach, he was able to solve every problem or nearly every problem correctly. When he did make a mistake, it was a simple computational error where he immediately recognized his own mistake. The method I taught him is the one most of us probably learned as children and not teaching it at all seemed peculiar to me. And in many instances, it removed millions of parents from being able to help their children.
Using Common Core involved implementing so many more steps that the problems took significantly more time and increased the chances of a computational error or the possibility of an increased writing error—not because of a lack of knowledge—but because of other factors that have less to do with math and more to do with sustained attention to tasks and other skills where boys are less likely to shine. The same could certainly happen with girls, but the challenges seem to happen to boys who are prone to moving and distractions.
When I told my son to use the method I learned as a child, he said, “I can’t. I’ll get in trouble.” There was a palpable fear of disappointing his teacher—of getting in trouble and being penalized for not solving a problem a specific way. Pleasing the teacher—to him—became more important than solving the problem.
At that moment, I asked my son to walk across the room and pick up a shoe he left by the sofa and return it to me. I then set a few chairs in his way and made him walk circuitously to get the other shoe and bring it back to me. I then asked him which way was the better way to get the shoe and why?
His response: “The first way because it is more direct.”
I asked, “do you think some people would like to go the other way?”
He said, “I guess, but why?”
The “new math” is like retrieving those shoes, but students are not being given the choice to pick the direct or circuitous routes across the room. For the most part, students are being given directives that disproportionately impacts boys. I found this peculiar because our educational institutions are always talking about differentiated instruction for children, the pedagogical approach that looks at employing strategies that helps each child thrive. That’s hard to do when classes are large and the tasks are using processes that may be less geared to boys.
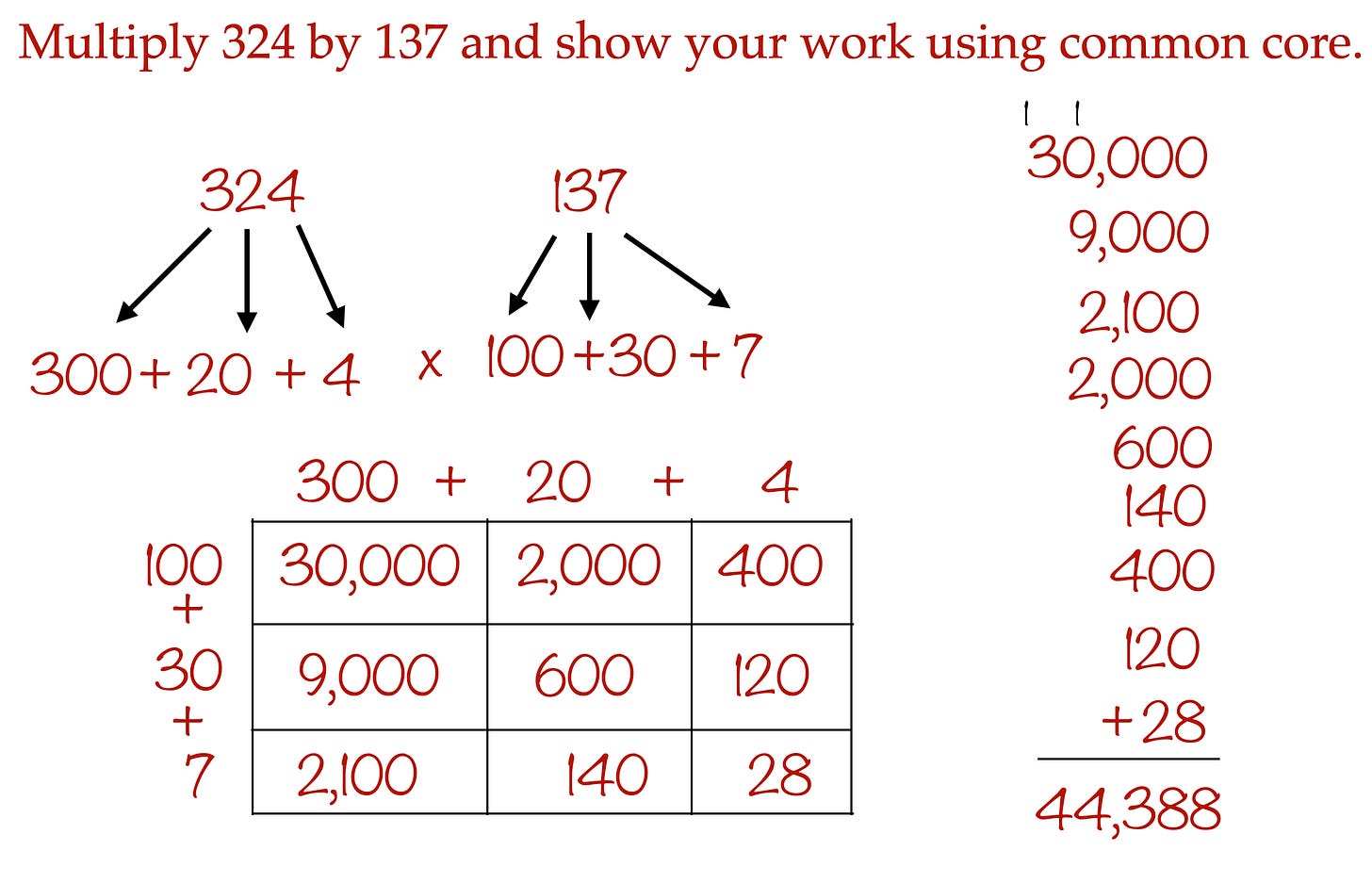
A multiplication problem using a Common Core approach might look like the two examples below in blue and red. One can see the circuitous routes that might trip a student up as many more steps are required. Because boys’ brains tend to operate in independent hemispheres and girls’ brains involve more cross-communication from one hemisphere to the next and back, these long sustained math approaches will favor them more so than boys.
The typical approach, at least the one I learned and display below, worked well for my son and required far fewer steps and allowed him to exercise his knowledge of multiplication more efficiently, at least for him. The examples above have some purpose as well when it comes to thinking about math in different ways that require varying degrees of reasoning. But when it comes to solving a problem, students need more than a one size fits all approach. When we restrict different tactics, the system imposes limitations on solutions in a world where there are many ways to solve problems and in a world where we need many people who can solve problems in different ways.
I once worked at a high school that used a program called the Interactive Mathematics Program (IMP). After years of use and declining math scores, the program was scrapped. Too often, students are the subjects of programs designed for the few but applied to the many.
Many of the other parents I spoke with were noticing the same challenges with Common Core. The Common Core approach engaged a host of other skills beyond math, like being able to write out problems horizontally down an entire page in layers and layers. And if one looks at handwriting in schools, one will also notice a difference between boys and girls in the aggregate. In the Common Core examples above, I solved them vertically and horizontally. In some instances, however, teachers wanted these problems solved vertically. A math problem that would take up 1/9 of a page would suddenly become a problem that would take up at least 1/3 of a page. Suddenly students were cramming their numbers onto the page.
Things like memorizing multiplication tables were a thing of the past. And as one father (who uses math for a living) shared with me, his daughter was not required to memorize her multiplication tables and certain math facts and—as a result— she has been uncomfortable with math ever since. Memorizing multiplication tables, one could argue, is like having sticky notes in the brain that aid students on their math journey.
The goal is not to introduce practices that favor some at the expense of others, but to introduce approaches that allow boys and girls to succeed and find a real love of learning while acquiring skills. Even if a student does not love math, giving students different ways to attack a problem allows for creativity and problem solving in more than one way and—at the least—a way to solve problems that helps them achieve goals and moves students toward a mental oriented model. By engaging learners with different approaches, teachers and parents can help students use the techniques that work best in crunch time.
The Common Core approach was used when the SAT changed its format in 2016 to include more reading into the math section, even as data across the U.S. then and now shows that boys are having a harder time with reading. Much of the thinking and rhetoric in the educational system is still geared toward girls because there is a cultural belief that they are behind (even though that is not the case) and so there are constant policy pushes to help girls advance, often while ignoring the outcomes of boys. Despite decades of boys’ poorer performance in reading, school districts, policy makers, and media are not placing as great a focus on boys’ needs as they do programs like girls in STEM.
When students are penalized for not using the “preferred methods” of solving a problem, boys who cut to the chase when it comes to solving math problems are penalized by feign egalitarianism. A student may get an answer wrong and receive more points on a test because the student followed the teacher’s method. Another student may use a different approach, show the work, and get the answer correct and get fewer points. This example may seem simple for the purpose of brevity, but it may well explain the reason girls—in instances—are surpassing boys in math, even as boys and girls are showing downward trends in math in many districts.
The graphs below follow the math progress of students who started in third grade in 2014-15 and will graduate in 2024. The data includes two school districts with different demographics as well as the state of California. (I would encourage parents in their districts to use this same approach or reach out to seank@gibm.us to analyze your district data).
Livermore Joint Unified School District: Data includes the progress of approximately 1,000 students who started in third-grade in 2014-15 and will graduate from high school in 2024.
Oakland Unified School District: Data includes the progress of approximately 2,200 students who started in third-grade in 2014-15 and will graduate in 2024.
California Schools: Data includes the progress of approximately 440,000 students who started in third-grade in 2014-15 and will graduate in 2024.

Educators and policymakers cannot argue the math-gap closed between boys and girls without first recognizing math scores decreased for both boys and girls. Even prior to COVID, math scores were trending downward. (It’s also important to recognize that some students may have left their district, left their schools, or left the state in any given year, but the student population is likely steady.)
Declining math scores were certainly exacerbated during COVID, but the decline was well on its way. While the data above follows student-sets that are likely many of the same students over time, other tests that do not follow the same students over time but large groups of students over time still show downward trends. In 2015, forty-percent of fourth graders scored proficient (33%) or advanced (7%) in math on the National Assessment of Educational Progress (NAEP), commonly referred to as the Nation’s Report Card. In 2019, four years later, thirty-four percent of eighth grade students scored proficient (24%) or advanced (10%) in math.
Although Livermore’s demographics differ from those of Oakland, the trend is seen in schools across the state, as the California data reveals that students’ math proficiencies were trending downward prior to COVID and were further exaggerated during COVID. While Livermore could argue that its scores were higher than the state averages, this too is more political than introspective because it fails to acknowledge the trends.
As one teacher in a school district told me:
“Administration was seizing on the opportunity to mention that their scores were better than the state average even as students were showing declines in performance and came from stable homes with extra-resources, of course they will score higher than state averages.”
It’s important that districts look at the increased proficiencies in its own schools as benchmarks that they hope to raise year after year with programs that are specific to academic progress. For the last several years, there is no denying schools have directed funding toward ideological efforts like grading equity, DEI, and new math programs—like Common Core and IMP—and have failed to improve academic outcomes on objective tests.
There is a way to get students to perform better and it will mean directing resources toward teachers and programs that show gains in educational progress by measuring student performance throughout the year, intervening with successful math specialists when students struggle, measure teacher success with boys and girls, and improve teacher training. Our resources need to go into the classroom with proven methods that are measurable and shareable with the public.
Here are a few suggestions for teachers and math.
Whenever possible, offer students more than one way to solve a problem.
If a student shows his work and gets the answer correct, do not penalize the student. Penalizing a student who gets a problem correct and shows his work demoralizes the student, stifles creativity, and further alienates him from the world of education, creativity, and problem solving.
If a student uses a particular method, award the student extra-credit for doing so or allow a student to redo the problems after the test when the pressure of getting answers correct is off the table and the student can focus on the method.
Track what methods boys and girls are using in your classes and see if you notice patterns. This is something you can actually do with your students.
Consider introducing a boys and girls learn differently approach into your classroom and your district.
There are many challenges facing our sons, and it’s important to get at the pedagogical approaches that help them best find success and acquire practical skills that aid them in problem solving. The Gurian Summer Institute is a great way to start looking at brain-based approaches to learning that help all students.
The program below is the perfect summer opportunity for teachers to learn more about a brain-based approach to learning that can help teachers and students thrive. The early-bird special closes on May 15.





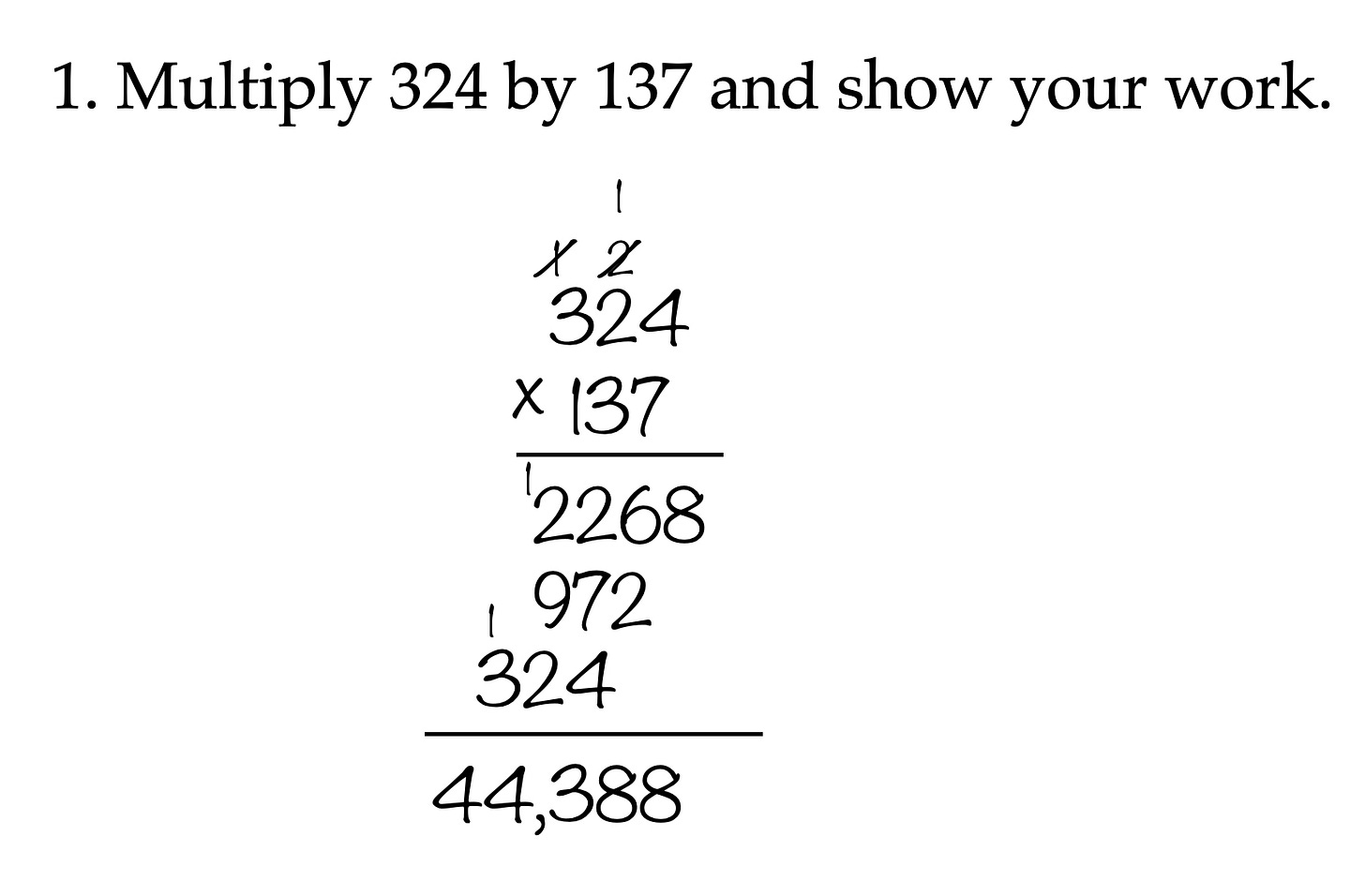



Sean, This is another right on the money article. The new math is circular, but to me, a woman, bizarre. It’s more than a couple of chairs in the way! My granddaughter was here for a week with homework lessons to tackle and I had trouble understanding and explaining the whole complicated procedure myself. I couldn’t understand why they made it so cumbersome never mind the “why” of it all. My husband, a former middle/high school math teacher even resorted to explaining things the old way. Even simple addition was a mess. Many of us, at best, only use up to geometry math in our lifetimes; examples; quilting, landscaping, balances finances, and cooking etc. In the end I showed my granddaughter the old method and she picked it up, but was concerned about her teacher. My other granddaughter is in the 4th grade and she is having trouble with division and multiplication. Took me all of five minutes to realize she hadn’t memorized her times tables. Why? Heck I have no idea. I told her this would help tremendously since it’s the founding principle for the next steps. Kinda like learning tablespoons and cup measurements is necessary to becoming a basic cook. Sean, this core math needs a few tweaks not just for boys, but for girls too! Thanks for all you do and your informative practical thinking!
https://www.youtube.com/watch?v=08v5C5DvR14